Reasoning-Grounded Natural Language Explanations for Language Models
(2025) Cahlik, V., Alves, R., and Kordik, P. World Conference on Explainable Artificial Intelligence 2025
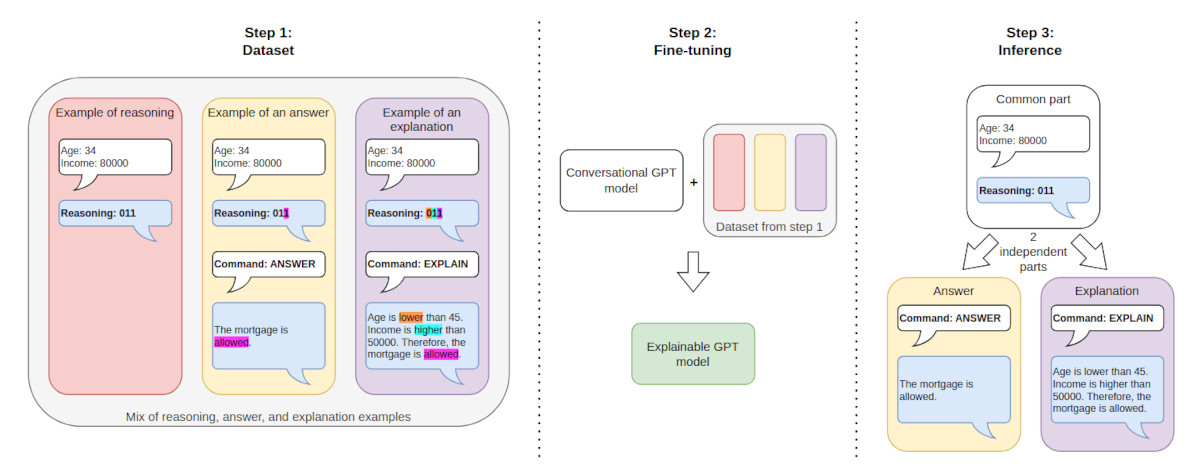
We propose a large language model explainability technique for obtaining faithful natural language explanations by grounding the explanations in a reasoning process. When converted to a sequence of tokens, the outputs of the reasoning process can become part of the model context and later be decoded to natural language as the model produces either the final answer or the explanation. To improve the faithfulness of the explanations, we propose to use a joint predict-explain approach, in which the answers and explanations are inferred directly from the reasoning sequence, without the explanations being dependent on the answers and vice versa. We demonstrate the plausibility of the proposed technique by achieving a high alignment between answers and explanations in several problem domains, observing that language models often simply copy the partial decisions from the reasoning sequence into the final answers or explanations. Furthermore, we show that the proposed use of reasoning can also improve the quality of the answers.
Links: Website, arXiv, PDF (preprint), Google Scholar, BibTeX, GitHub, Zenodo
Adapting the Size of Artificial Neural Networks Using Dynamic Auto-Sizing
(2022) Cahlik, V., Kordik, P., and Cepek, M. 2022 IEEE 17th International Conference on Computer Sciences and Information Technologies (CSIT), pp. 592-596. IEEE.
We introduce dynamic auto-sizing, a novel approach to training artificial neural networks which allows the models to automatically adapt their size to the problem domain. The size of the models can be further controlled during the learning process by modifying the applied strength of regularization. The ability of dynamic auto-sizing models to expand or shrink their hidden layers is achieved by periodically growing and pruning entire units such as neurons or filters. For this purpose, we introduce weighted L1 regularization, a novel regularization method for inducing structured sparsity. Besides analyzing the behavior of dynamic auto-sizing, we evaluate predictive performance of models trained using the method and show that such models can provide a predictive advantage over traditional approaches.
Links: IEEE Xplore (published version), PDF (preprint), Google Scholar, BibTeX, GitHub
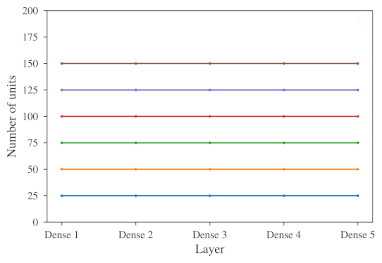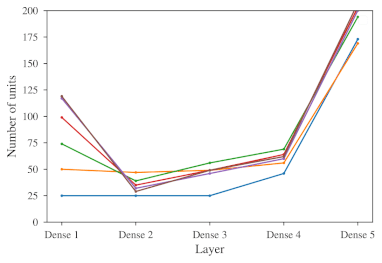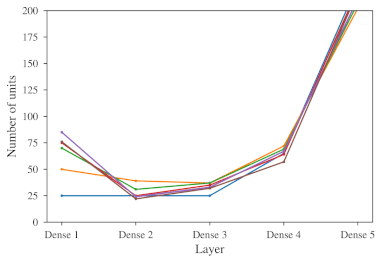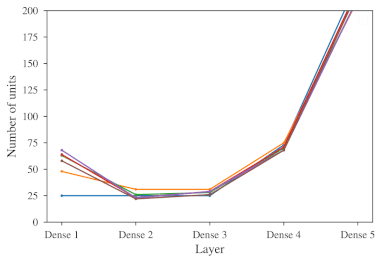
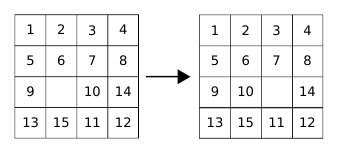
Near Optimal Solving of the (N2-1)-puzzle Using Heuristics Based on Artificial Neural Networks
(2021) Cahlik, V. and Surynek, P. Computational Intelligence. IJCCI 2019. Studies in Computational Intelligence, vol 922., pp. 291-312, Springer, Cham.
We address the design of heuristics for near-optimal solving of the (N2–1)-puzzle using the A* search algorithm in this paper. The A* search algorithm explores configurations of the puzzle in the order determined by a heuristic that tries to estimate the minimum number of moves needed to reach the goal from the given configuration. To guarantee finding an optimal solution, the A* algorithm requires heuristics that estimate the number of moves from below. Common heuristics for the (N2–1)-puzzle often underestimate the true number of moves greatly in order to meet the admissibility requirement. The worse the estimation is the more configurations the search algorithm needs to explore. We therefore relax from the admissibility requirement and design a novel heuristic that tries estimating the minimum number of moves remaining as precisely as possible while overestimation of the true distance is permitted. Our heuristic called ANN-distance is based on a deep artificial neural network (ANN). We experimentally show that with a well trained ANN-distance heuristic, whose inputs are just the positions of the tiles, we are able to achieve better accuracy of estimation than with conventional heuristics such as those derived from the Manhattan distance or pattern database heuristics. Though we cannot guarantee admissibility of ANN-distance due to possible overestimation of the true number of moves, an experimental evaluation on random 15-puzzles shows that in most cases the ANN-distance calculates the true minimum distance from the goal or an estimation that is very close to the true distance. Consequently, A* search with the ANN-distance heuristic usually finds an optimal solution or a solution that is very close to the optimum. Moreover, the underlying neural network in ANN-distance consumes much less memory than a comparable pattern database. We also show that a deep artificial neural network can be more powerful than a shallow artificial neural network, and also trained our heuristic to prefer underestimating the optimal solution cost, which pushed the solutions towards better optimality.
Links: SpringerLink (published version), PDF (preprint), Google Scholar, BibTeX, GitHub
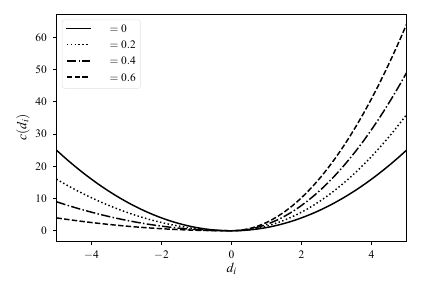
On the Design of a Heuristic based on Artificial Neural Networks for the Near Optimal Solving of the (N2-1)-puzzle
(2019) Cahlik, V. and Surynek, P. Proceedings of the 11th International Joint Conference on Computational Intelligence (IJCCI 2019), pp. 473-478, Vienna, Austria, SciTe Press.
This paper addresses optimal and near-optimal solving of the (N2–1)-puzzle using the A* search algorithm. We develop a novel heuristic based on artificial neural networks (ANNs) called ANN-distance that attempts to estimate the minimum number of moves necessary to reach the goal configuration of the puzzle. With a well trained ANN-distance heuristic, whose inputs are just the positions of the pebbles, we are able to achieve better accuracy of predictions than with conventional heuristics such as those derived from the Manhattan distance or pattern database heuristics. Though we cannot guarantee admissibility of ANN-distance, an experimental evaluation on random 15-puzzles shows that in most cases ANN-distance calculates the true minimum distance from the goal, and furthermore, A* search with the ANN-distance heuristic usually finds an optimal solution or a solution that is very close to the optimum. Moreover, the underlying neural network in ANN-distance consumes much less memory than a comparable pattern database.
Links: SciTePress (published version), PDF (preprint) , Google Scholar, BibTeX, GitHub